发表日期：2018-11-17  精选文章

新手必看：数据科学家必学必会的 5 个基本统计概念

—— 利用统计学，我们将能以一种更有针对性，更”信息驱动“的方式来处理数据。这其中涉及的数学知识能帮助我们形成关于数据的具体结论，而不仅仅是猜测。使用统计数据，...

---

在数据科学的世界里，如果数据科学家是魔法师，那统计学就是他们的魔杖。

总的来说，统计，就是利用数学对数据进行技术性分析。当然，像条形图这样的简单可视化图像也能给你提供一些高等级的信息，但利用统计学，我们将能以一种更有针对性，更”信息驱动“的方式来处理数据。这其中涉及的数学知识能帮助我们形成关于数据的具体结论，而不仅仅是猜测。

使用统计数据，我们可以获得更深入、更细微的洞察能力，可以了解我们的数据是如何构建的。在了解结构的基础上，我们将能发现应用其他数据科学技术的最佳方式，并以此获取更多信息。

今天，我们将一起了解数据科学家必学必会的5个基本统计概念，以及如何最有效地应用它们！

统计特征

统计特征可能是数据科学中最常用的统计概念之一。它通常是你在探索数据集时使用的第一种统计技术。常见的统计特征包括偏差、方差、均值、中位数、百分位数等等。它们其实非常容易理解，也很容易在代码中实现！

让我们看看下面这个图吧：

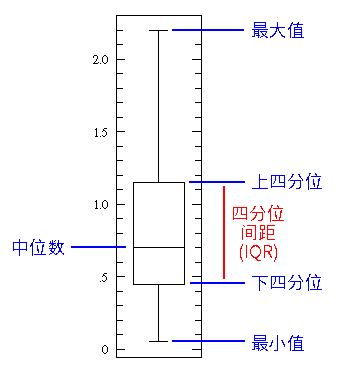
一个简单的箱形图

中间的这条横线是数据的中位数。相对于平均数，中位数在数据中有异常值的时候能更加忠实地反应数据的特征。下四分位数基本上是数据的 25% 点，也就是数据中 25％ 的点低于该值。上四分位数是数据的 75% 点，也就是数据中 75％ 的点低于该值。最小值和最大值表示数据范围的上端和下端。

箱形图能很好地表现出基本统计特征的用途：

• 如果箱形图很短，就意味着你的大部分数据点都很相似，因为很多数据都集中在很小的范围内
• 如果箱形图很长，就意味着你的大部分数据点都差异很大，因为这些值分布在很宽的范围内
• 如果中位数接近底部，那么我们就能知道大多数数据具有较低的值。如果中位数接近顶部，那么我们就能知道大多数数据具有更高的值。基本上，如果中位数不在框的中间，则表明数据存在偏斜。
• 图中方框上下的“胡须”会不会很长？这意味着数据具有较高的标准差和方差，也就是说数值分散且变化很大。如果方框的一侧有“胡须”，而另一侧没有，那么数据可能只在一个方向上变化很大。

上面这些信息，都来自这几个易于计算的简单统计特征！如果你需要对数据进行快速又翔实的分析，请务必先试着分析一下统计特征。

概率分布

我们可以将概率定义为某个事件发生的几率。在数据科学中，这个几率通常被量化成在 0 到 1 之间的数字。其中 0 表示我们确定它不会发生，1 表示我们确定它肯定发生。那么，概率分布就是表示实验中所有可能值的概率的函数。 让我们看看下面这三张图：

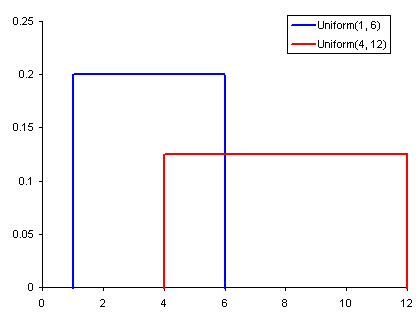
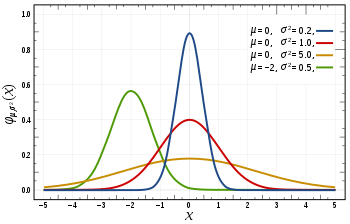
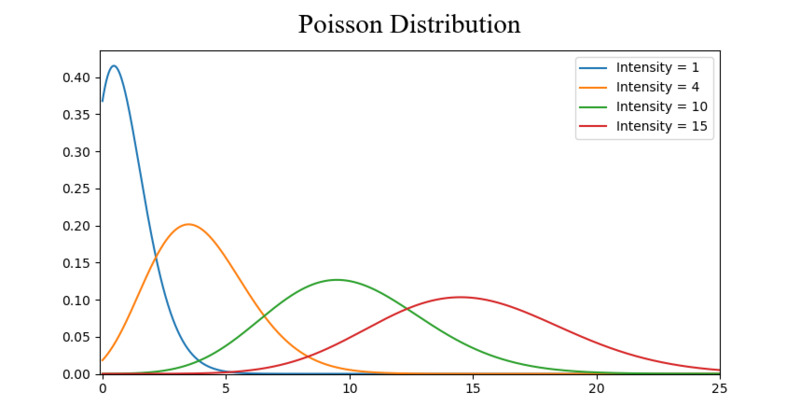
常见概率分布：均匀分布（上）、正态分布（中）、泊松分布（下）

• 均匀分布是上面 3 张图中最简单的。它有一个值，而且只出现在一定范围内，超出该范围的都是 0。这是一种“开关”分布——每个点要么有数据，要么是0。我们还可以将其视为只有 0 和某个数值的分类变量。同样，如果某个分类变量具有除 0 以外的多个值，我们也可以将其视为多个均匀分布组成的分段函数。
• 正态分布，通常也称为高斯分布，是由其平均值和标准差定义的。平均值改变分布的空间高度，而标准差控制分布的扩散程度。 与其他分布（例如泊松分布）的重要区别在于，正态分布的标准差在所有方向上是相同的。 因此，利用高斯分布，我们能了解到数据的平均水平，以及数据的散布范围——比如它是分散在较大范围里，还是高度集中在几个值附近。
• 泊松分布类似于正态分布，但具有附加的偏斜量。 当偏斜量很低的时候，泊松分布将在所有方向上都具有相对均匀的扩展，就像正态分布一样。但是当偏斜量较大时，数据在不同方向上的分散程度会有所不同——在一个方向上它将非常分散，而在另一个方向上它将高度集中。

除此之外，还有更多不同的概率分布值得你深入研究，但目前这 3 个分布模式已经很有用啦。比如，我们可以使用平均分布模型来快速查看并解释分类变量。如果看到数据呈高斯分布，那么我们就应该选择那些特别适用于高斯分布的算法来处理它们。而对泊松分布，我们就必须特别小心地选择算法，以便在空间分布不均匀的时候也能可靠地处理数据。

降维技术

降维这个词应该不难理解，大家应该都听过“降维打击”吧？没错，就是拍扁（误。

举例来说，对一个很复杂的数据集，我们希望减少它的维度。在数据科学中，这主要是特征变量的数量。以下图为例：

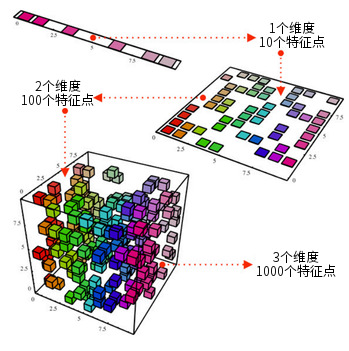
一个降维的示意图

上面这个立方体代表了一个 3 维的数据集，里面大约有 1000 个特征点。当然，以现在的计算能力，分析 1000 个点基本上是小菜一碟，但对于更大尺度上的数据集，还是可能碰到一些问题的。然而，如果我们从 2 维角度来分析其中的数据——就像只从立方体的某个面看进去——我们就能从这个角度很轻易地区分各种不同颜色的数据点。在降维技术的帮助下，我们就像是把 3 维的数据集投影到一个 2 维平面上，再进行操作。这能相当有效地减少需要计算的特征点的数量——现在只剩 100 个啦！

另外一种降维的思路，是特征修剪。在进行特征修剪的时候，我们希望能去除那些对分析结果无关的特征。举例来说，假如在探索数据的时候，我们发现有 10 个特征，其中 7 个与输出有很高的相关性，另外 3 个的相关性很低。那么，这 3 个低相关的特征或许并不值得我们分析，可能可以直接从分析中去掉，而不影响最后的输出。

在降维操作中，最常见的统计技术是 PCA（Principal Component Analysis，主成分分析）。它实际上是通过创建各种特征的矢量，标明它们对输出结果的重要性，即它们的相关性。PCA 在上面讨论的两种降维方式中都发挥着重要的作用。 在这里你能看到更多关于 PCA 的详细介绍。

过采样和欠采样

过采样（Over Sampling）和欠采样（Under Sampling）是用于分类问题的统计技术。有时，我们的分类数据集可能会太过偏向其中的一侧。例如，我们在第1类中有2000个样本，但在第2类中只有200个。这将严重影响我们尝试用于建模和预测的许多机器学习技术！因此，我们可以使用过采样和欠采样技术来解决这个问题。请看下面的示意图：

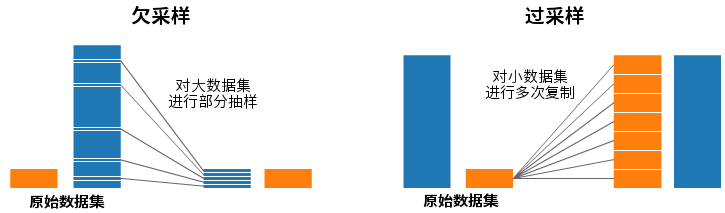
欠采样（左）和过采样（右）

在上面的两张图中，蓝色的样本数量都大大超过了橙色。在这种情况下，我们可以通过两种预处理方法对样本进行处理，以构建机器学习所需的模型。

欠采样意味着对于量多的一类，我们只抽取其中的一部分数据，组成一个和量少的那类相当的数据集。如果你需要保持样本概率分布的一致性，那你就该选择这种采样方式。是不是很简单？这样两类样本的数量就平衡了！

过采样就刚好相反，我们将总量较少的那类样本复制多次，以便该类样本的总数和多的那类一致。在复制的过程中，应当保证不改变这类样本的分布情况。这样，我们在没有引入额外数据的情况下，使两类样本的数量平衡了！

贝叶斯统计学

要想完全理解我们为什么使用贝叶斯统计学，首先就得了解频率统计的问题在哪里。频率统计是大多数人在听到“概率”一词时所考虑的统计数据类型。它涉及到应用数学来分析某些事件发生的概率，具体而言，我们计算的唯一数据是先验数据。

拿骰子做例子吧。假设我给了你一个骰子，并问你扔出6的几率有多大，我想大多数人都会直接说出是六分之一。事实上，如果我们要按频率统计的方法进行分析，就得真的统计 10000 次掷骰的结果，并计算每个数字的频率——最后结果差不多在 1/6 上下！

但如果有人告诉你，给你的这个特定的骰子其实灌了铅，保证每次都会投出 6，那又会如何呢？既然频率统计只考虑先验数据，那么这条关于骰子的信息并不会被纳入统计结果中。

而贝叶斯统计会将这些证据纳入统计计算中。看看贝叶斯定理公式吧：

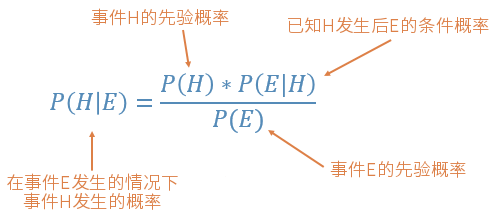
在上面这个公式中，P(H) 的概率就是频率统计分析的结果，按照先验数据统计得出事件 H 发生的概率；而 P(E|H) 被称为`似然性`，也就是这个证据正确与否的概率，也是根据频率分析提供的信息得来的。

在上面灌铅骰子的例子中，假设你想要投 10000 次骰子，然后投出的前 1000 个值都是 6——那么你应该不可能不觉得这个骰子有问题吧。

最后，P(E) 则是这个证据本身出现的概率。如果我告诉你骰子是灌铅的，你能在多大程度上相信我，还是你会觉得这只是一个陷阱呢？

如果我们的频率统计没有问题，那么统计结果就会支持“每骰必 6”的猜测。而于此同时，我们又将灌铅骰子这个证据纳入考量，这个证据的正确与否都基于它本身的频率统计先验数据。

从方程的结构，我们可以看出，贝叶斯统计将上述的一切可能性都考虑在内了。所以，如果你认为先前的数据不能很好地代表未来的数据和结果，请考虑使用贝叶斯统计方法。

怎么样，今天提到的 5 个统计学概念，大家都了解了吗？

最后，我想用一个我最喜欢的数据科学笑话结尾，希望大家喜欢：

“世界上有两种类型的数据科学家：一是可以从不完整的数据中推断出结果的人。”

（本文已投稿给「优达学城」。 原作： George Seif 编译&图片汉化：欧剃 转载请保留此信息）

编译来源： https://towardsdatascience.com/the-5-basic-statistics-concepts-data-scientists-need-to-know-2c96740377ae

标签：Udacity、Translate、Data-Science