发表日期:2020-02-06
一文搞懂RL!在现实生活中,强化学习是怎么解决问题的?
—— 强化学习是人工智能领域最重要的工具之一,但不是这个行业的人,可能对强化学习的概念依旧不熟悉。今天将用现实生活中例子来解释这个机制
作者:Sterling Osborne
如果你不是身处机器学习行业,或许你依旧会觉得这一切离我们的生活都非常遥远。但如果告诉你。强化学习技术,可以让计算机基于既定预算和个人偏好,安排一群人的聚餐计划,是不是就很贴近日常生活了?
没错,强化学习技术可以被用于解决类似上面这样的日常规划问题,包括旅行计划、预算安排和商业决策等等。它的优势在于:
- 能将各种结果的概率都纳入考量
- 能让我们对部分环境进行控制。
为了让大家更好地了解如何使用强化学习来解决日常工作中遇到的问题,今天我们就从一个简单的例子展开说。
01. 强化学习是什么
在这之前,我们先来了解下强化学习的概念。
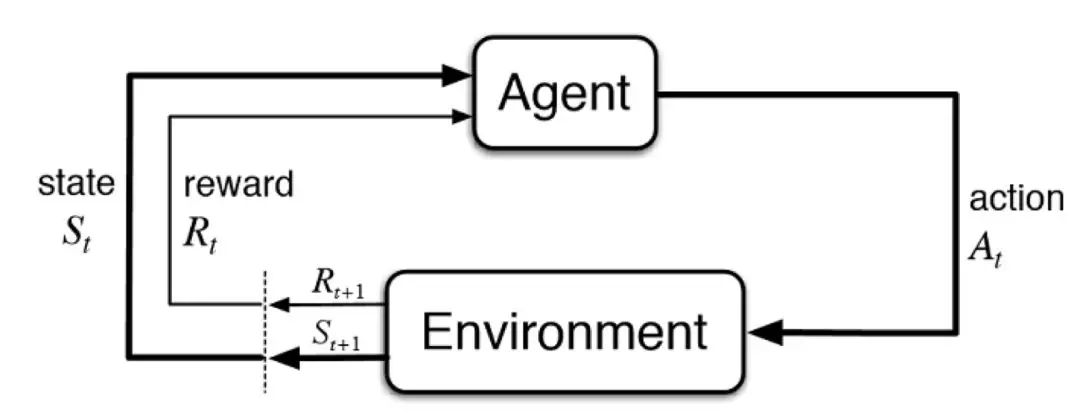
强化学习(Reinforcement learning,简称 RL)是机器学习中的一个领域。
它通过基本的试错过程,针对环境的每个特定状态,寻找最优的行动方式。机器学习模型将在一开始引入一个随机的规则,同时在每次做出行动的时候给模型输入一定量的分数(这被称为奖励)。
这个过程将不断重复,一直到模型达成了某个目标(比如一场游戏赢了或是输了),于是这一轮(或这一回合,Episode)就结束,游戏重置到初始状态。
随着模型运行回合的不断重复,它将会记住哪些行为更有可能导向更优的结果,由此找到某个给定状态下的最优行为,也就是最优策略。
许多在线的 RL 应用会使用游戏或是虚拟环境来训练模型,模型在其中可以反复和环境产生互动。
举个例子🌰,你让一个模型反复玩井字棋游戏,它就会通过观察游戏结果,不断调整自己的策略。
但在现实生活中,我们往往无法用这种方式来训练模型。比如,在线购物网站的推荐系统需要人类用户的反馈,才能知道推荐是否合适。而且,训练数据来源也会受到与网站互动的用户数量限制。
这个时候,我们一般会用一些能体现消费趋势的采样数据,生成一个估计概率。
通过这种方式,我们可以创建部分可观测的马尔可夫决策过程(Partially Observed Markov Decision Process,缩写 POMDP),作为概括潜在概率分布的方法。
部分可观测的马尔可夫决策过程(POMDP)
马尔可夫决策过程(Markov decision processes,MDP)提供了一个架构模型,以在最后的结果只有一部分能由决策者控制(而另一部分随机)的情况下进行决策。
MDP 的关键特征在于:它们遵循马尔可夫性质,未来的状态和过去的状态没有关联。也就是说,进入下一个状态的概率只依赖于当前状态。
POMDP 的工作方式与之类似,唯一区别是,它只是 MDP 的概括。简而言之,这个模型不是简单地与环境交互,而是根据观察到的结果给出一个概率分布集。你可以在 pomdp.org 上查到更详细的信息。
一般来说,我们可以在 POMDP 上使用值迭代方法,但今天这个例子中,我们决定使用蒙特卡罗学习(Monte Carlo Learning)。
02. 示例环境
假设在学校的一间教室里,老师对于废纸的处理有非常严格的规定,任何一张废纸都必须传到老师的讲台上,然后由老师丢进废纸篓里。
然而,有些学生却不大规矩,他们懒得把纸传来传去,偶尔会直接从座位上把纸团往纸篓里“投篮”。这种行为会激怒老师,并遭到惩罚。
这样就形成了一个非常基本的行为-奖励对应机制,我们可以把这样的教室环境简化成下面这样的示意图:
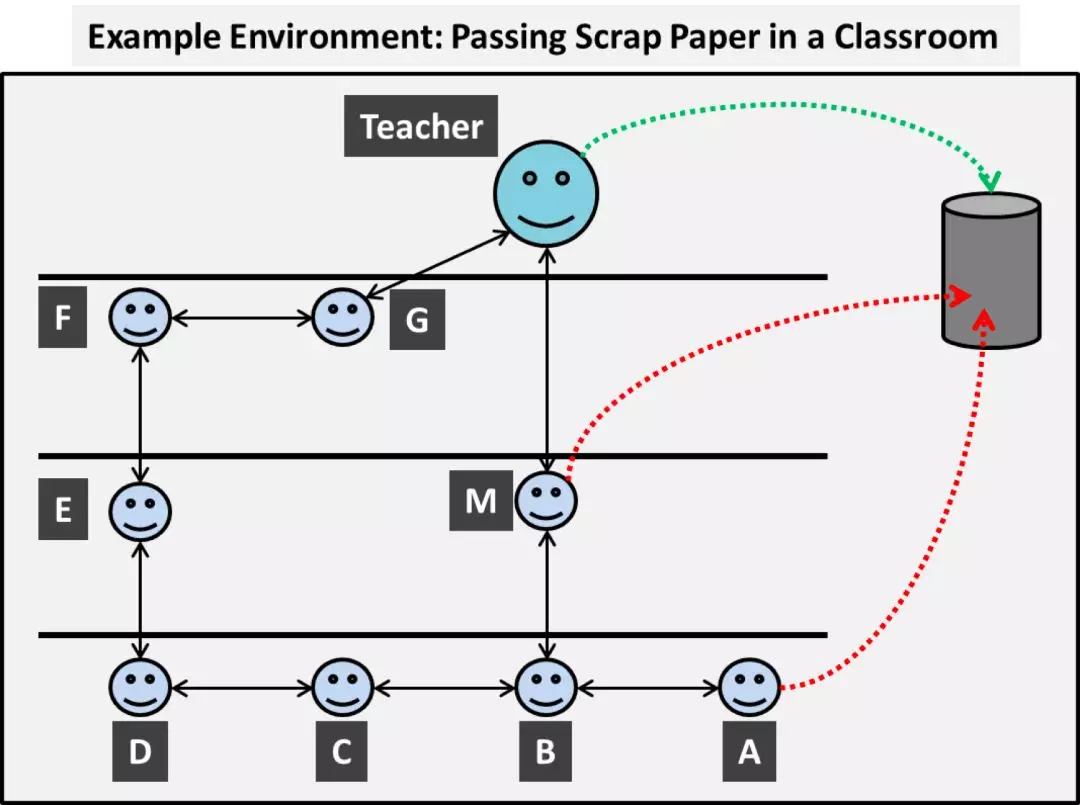
我们的目标是,让 AI 找到每一个学生应该如何行动,才能将纸张传给老师,避免发生“投篮“事件。
状态(States)与动作(Actions)
在这个环境中,每一个人都被认为是一个状态,他们都各自有一系列可执行的动作:将纸张传递给相邻的人,留在手上,或(有些人)把纸投向纸篓。因此,我们可以把环境用下面这样的网格图来表示(这是更加标准的表示法):
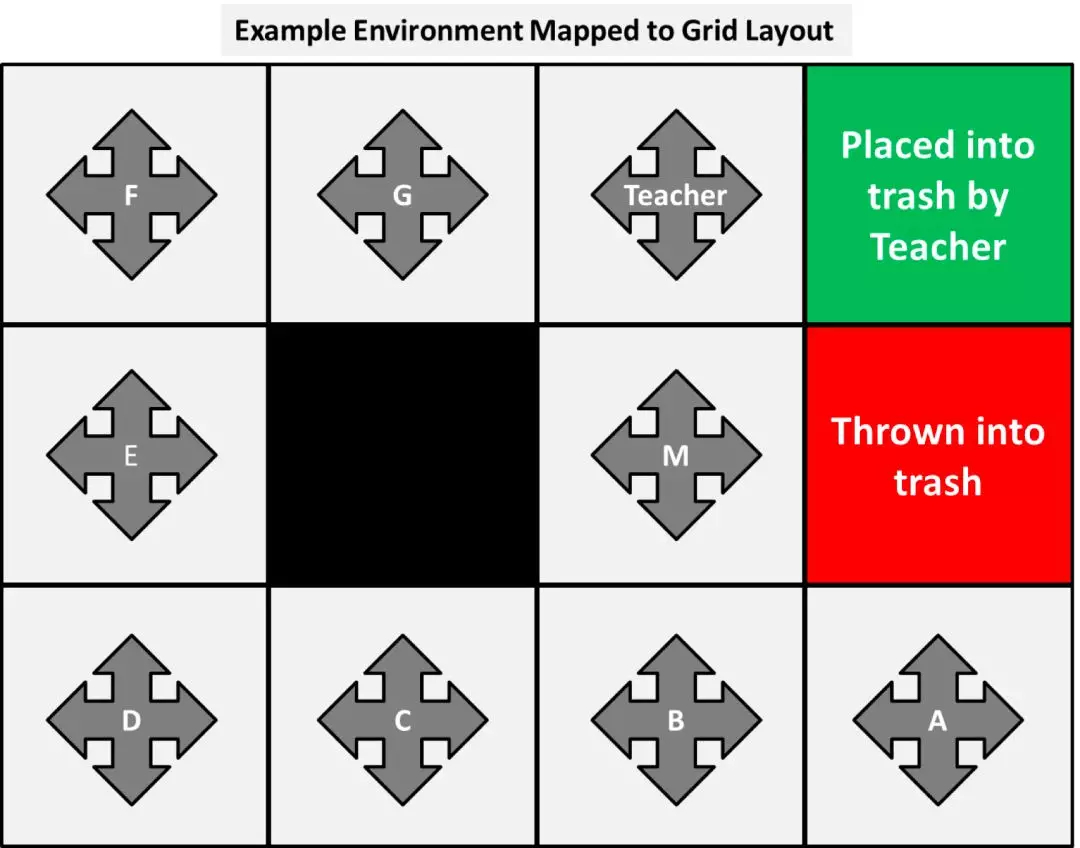
设计成这样的原因是,这样每一个人(状态)都有上下左右 4 个动作可选,每个动作都对应实施者的一个“真实”行为:
将纸张传递给箭头方向的人,或是投向纸篓。指向墙壁的那些动作(包括指向中间无人的黑色区域)则代表这个人将纸条留在手上不动。在有些情况下,这个动作会和其他重复,但对于我们这个例子来说,这并不会造成什么问题。
举例而言,A 的 4 个动作选项分别是:
- 上 = 抛进纸篓
- 下 = 留在手上
- 左 = 传给 B
- 右 = 留在手上
概率性环境(Probabilistic Environment)
目前,能够部分影响环境的决策者还都是我们。我们将告诉每一个学生他们应该采取的行为,这被称为策略(policy)。
要想掌握强化学习,首先要面对的一大挑战就是,如何理解环境的概率性,以及它背后的意义。一个概率性的环境意味着,当我们依照策略,要求某个状态,采取某个动作的时,这个动作是否真的会被实施,其实是有一定概率的。
换成人话说,比如我让 A 把纸张传递给 B,但 A 可能并不会按照策略中要求的那样行动,而选择了直接把纸投向废纸篓。
生活中的例子是,当我们在购物网站上给用户推荐商品的时候,用户也不一定老老实实地点开每一个页面。
可观测转移概率(Observed Transitional Probabilities)
为了找到可观测转移概率,我们需要收集一些样本数据,以了解环境的行为。在收集数据之前,我们先引入一个随机的初始策略。下面是一个随机选取的策略,它看起来能得到挺不错的结果:
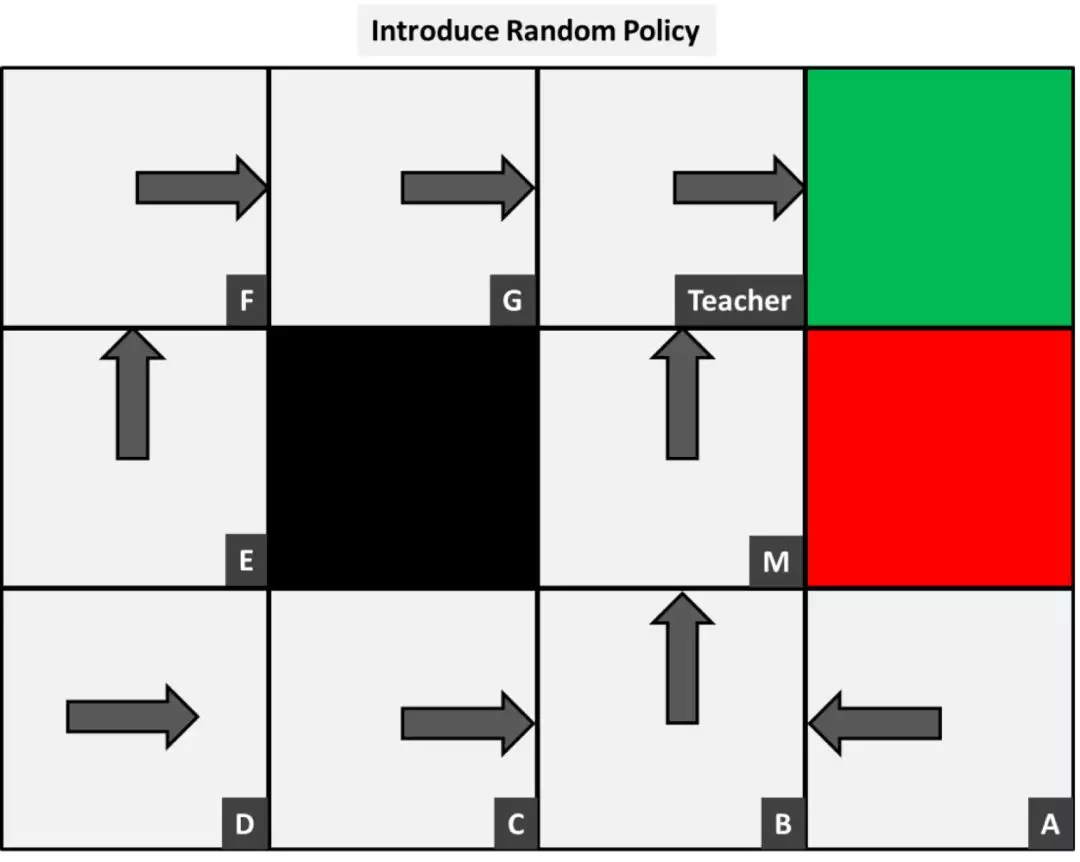
然后,我们观察每个人在这个策略下采取的行动。比如坐在教室的最后一排,数出 A 对纸张的处理行动次数:
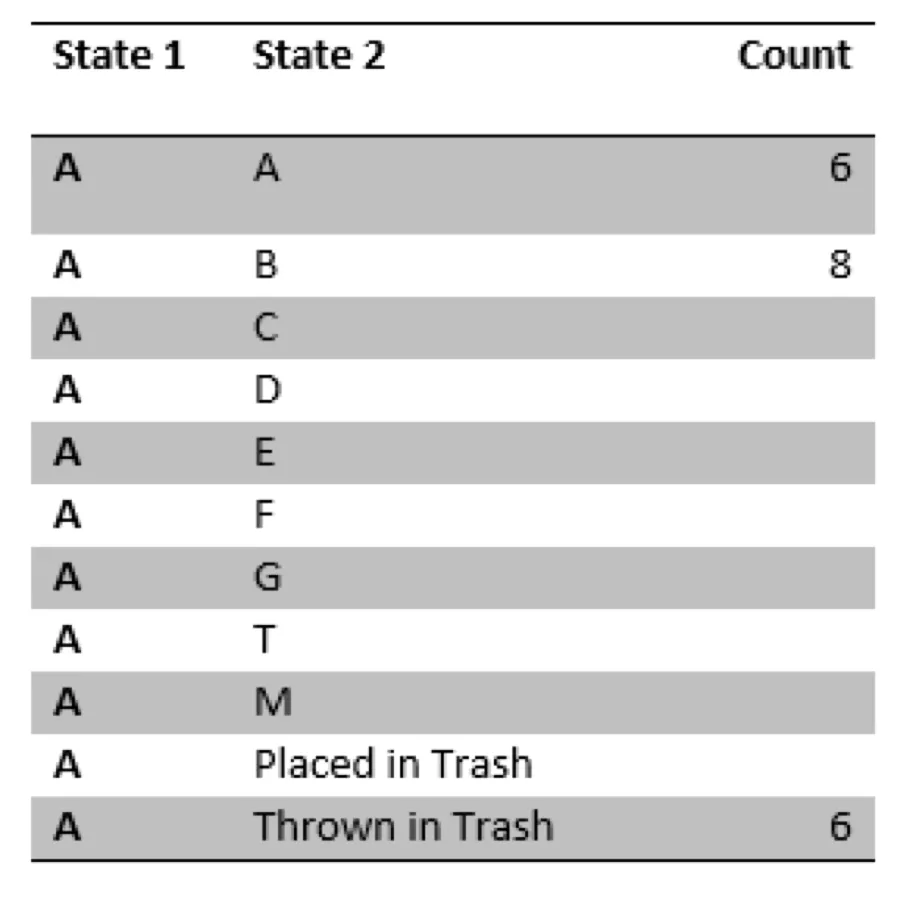
经过观察我们发现,纸张经过 A 共 20 次,其中 6 次 A 把纸张留在自己手上,8 次传给了 B,另外 6 次直接丢向了纸篓。
这就意味着,在我们的初始政策下,A 留下纸张和投向纸篓的概率都是 6/20=0.3,而传给 B 的概率是 8/20=0.4。
同理,我们对教室里的所有人都进行观察记录,得到了以下的采样数据:
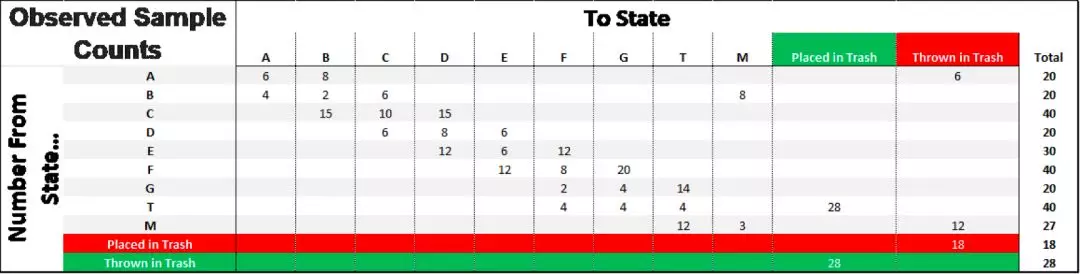
观测到的实际结果
我们将每个结果的对应概率计算出来,并使用这个概率来模拟一个环境。
这个模型的准确率,很大程度取决于,从样本中计算得到的概率是否能真实代表整个环境。也就是说,我们需要确保样本数量足够大,足够丰富。
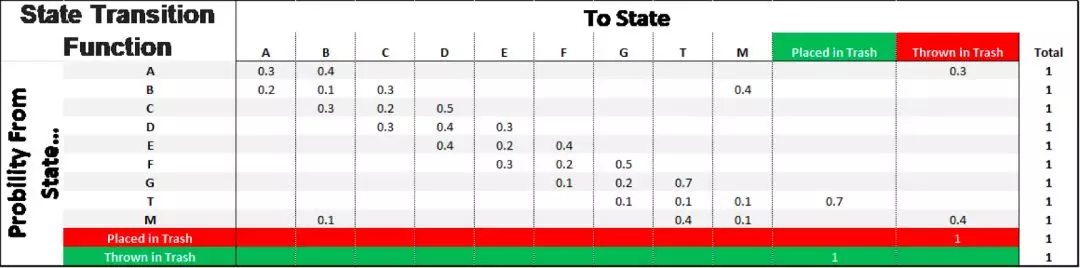
观测到的转移概率函数
03. 多臂老虎机问题、回合、奖励、回报以及折扣因子
(Multi-Armed Bandits, Episodes, Rewards, Return and Discount Rate)
现在,我们已经根据 POMDP 下的样本数据估算了转移概率。下一步,在放进任何一个模型之前,我们要先设置好奖励。
至今为止,我们只讨论了最后一步的结果:纸被老师放进废纸篓,并产生一个正向奖励;或是纸被 A 或 M 投了出去,则产生一个负向的奖励。在回合结束时的这个最后奖励被称为终止奖励(Terminal Reward)。
但除此之外,还有第三种不那么理想的结果:纸被不断地传来传去,却从来没有(或是拖了很长很长时间才)被传递/投到纸篓里。
因此,我们总共会有 3 种不同的结果:
- 纸被老师放进废纸篓,并产生一个正向终止奖励
- 纸被一个学生投向废纸篓,并产生一个负向终止奖励
- 纸被不断地传来传去,或是长时间停在某个学生手上,远超正常所需的时间
为了避免出现“投篮”操作,我们给这种行为加上一个很大的负向奖励,比如 -1。由于老师要求纸张传到前面再放进纸篓,所以我们给这种行为加上一个很大的正向奖励,比如 1。
为了避免上面说的第三种情况,我们给每个动作都加上一个比较微小的负向奖励,比如 -0.04。
如果我们把这个值设置成正数或是零,模型就可能会让纸张在教室里无止境地转呀转,毕竟获得一些小奖励比面对最后可能是负数的结果好多了。
但负得太多也不行,所以这个数字的绝对值必须足够小,这样即使整个过程可能花上很多步骤,最后得到的正向奖励也不会被这中间步骤的负向奖励给抵消掉。
请注意,奖励的数字总是相对的。作为例子,我只是随意选择的数字,如果结果不理想,你就需要对它们进行调整。
虽然我们上面反复提到了回合(episode),但我们还没正式定义它。在我们这个例子里,一个回合就是一张纸从某人手上开始,被传递着穿过教室,抵达(或被投掷到)废纸篓的整个过程。当纸被传递到或是投掷到废纸篓时,就进入了终止状态,这个回合也就结束了。
在其他的例子里,比如玩井字棋的时候,终止状态就是游戏胜负已定的时候。
由于需要丢弃的废纸从理论上说可能出现在任意状态,所以我们需要足够多的回合对模型进行重复训练,以确保每一种状态和行动都被覆盖到,保证最终结果的有效性。
然而从另一方面考虑,引入的回合越多,需要进行的计算量也越大,对于一些复杂或是大尺度的环境来说,用于计算的资源并不是无限的。
这也就是所谓的多臂老虎机问题(Multi-Armed Bandit problem):在时间等资源有限的条件下,我们需要对每个状态的每个行动都进行测试,以使我们的策略能够选择出最优化的行动。
换句话说,我们需要验证带来好结果的行动实际上就是正确的选择,而不只是运气好;反之那些带来坏结果的行动确实就是很糟糕的。
当然,在我们现在这个例子中,因为只有不多的几个状态,看起来还是很简单的。但如果这些状态的数量成倍地增加呢?
强化学习模型的总体目标就是选择能最大化预期累积奖励(expected cumulative rewards)的行动——即寻求所谓的回报(return)。
换句话说,回报就是一整个回合运行过程中获得奖励的总数。最简单的统计回报的办法就自然是,把每一个回合中得到是所有奖励都加起来,包括最后的终止奖励。
而一种更严谨的计算方式是:假定每个回合中,第一步行动的重要性最高,之后逐渐减少。于是在计算公式中,我们给每一步的奖励都乘上一个折扣因子 γ(gamma):
<img src=”https://cdn.jsdelivr.net/gh/oicebot/oicebot.github.io/img/20200206/009.webp” width=100%>
也就是说,我们还是把所有的奖励都加在一起,但对于越往后的步骤,通过乘上折扣因子使其奖励的权重越小。
对于我们这个例子来说,这就像是老师会按照一个回合中参与行动的顺序,对所有参与者进行奖励(或是处罚)。
比如,一张纸从 A出发,传给 B,然后到 M,最后被 M 远程投到废纸篓里。受到处罚最重的自然是 M,其次是把纸条传给 M 的 B,而 A 虽然也参与了,但比 M 和 B 轻得多。
这也导致一个回合经过的时间越长(步数越多),得到的奖励或惩罚的绝对值就会更少——但由于步骤增加,积累的负面奖励就会更多。
04. 在这个例子中应用模型
因为这个例子中的环境非常小,所以我们可以手动计算出部分结果,并举例说明改变参数会带来哪些变化。
对于任何一个算法,我们都需要初始化一个状态价值函数(state value function)V(s),我们决定把每个节点都初始化为零:

接下来,我们让模型基于我们观测到的概率分布,模拟环境运行情况。模型将从一个随机位置开始,将我们的策略在概率环境中执行,并计算结果。
下面是头三次模拟的情况:
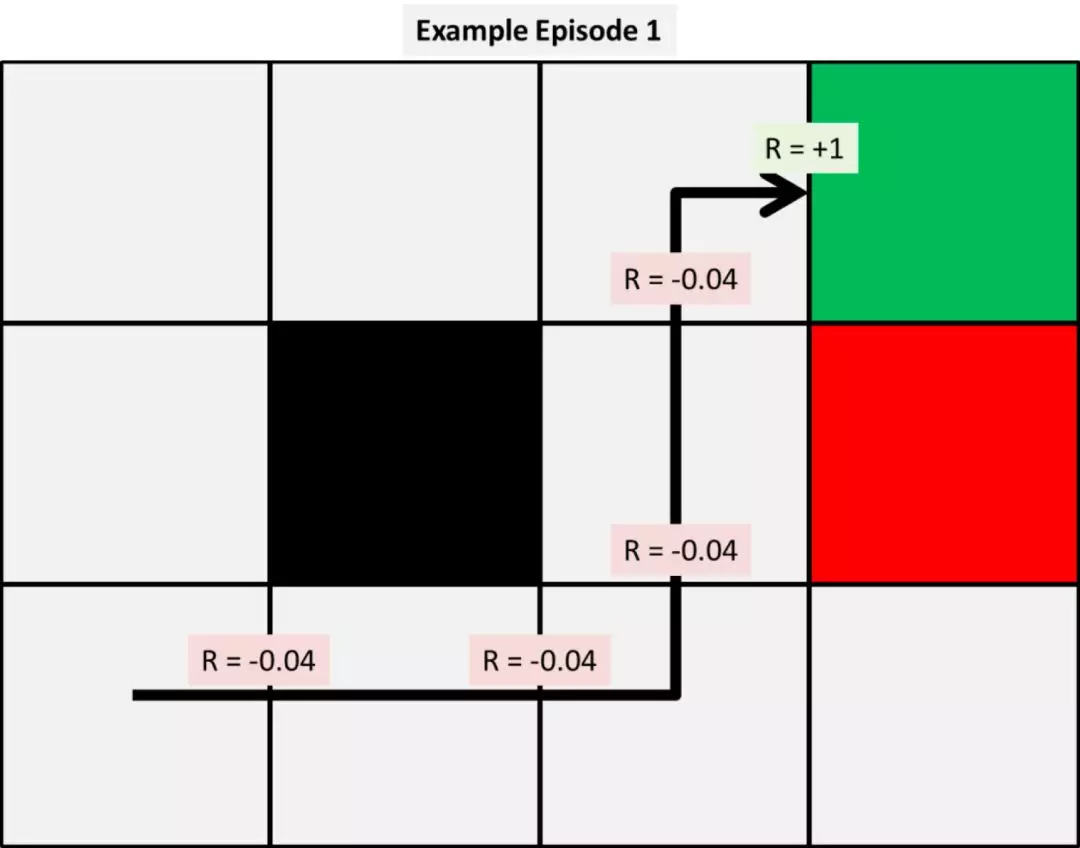
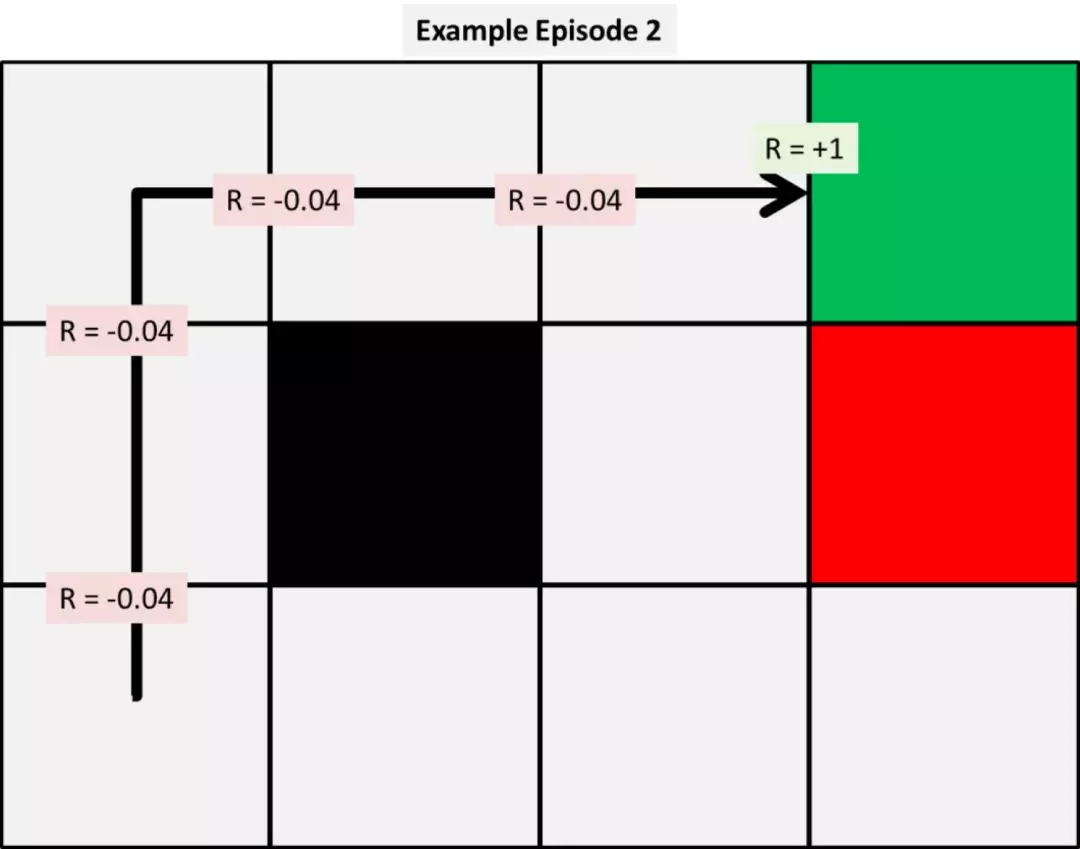
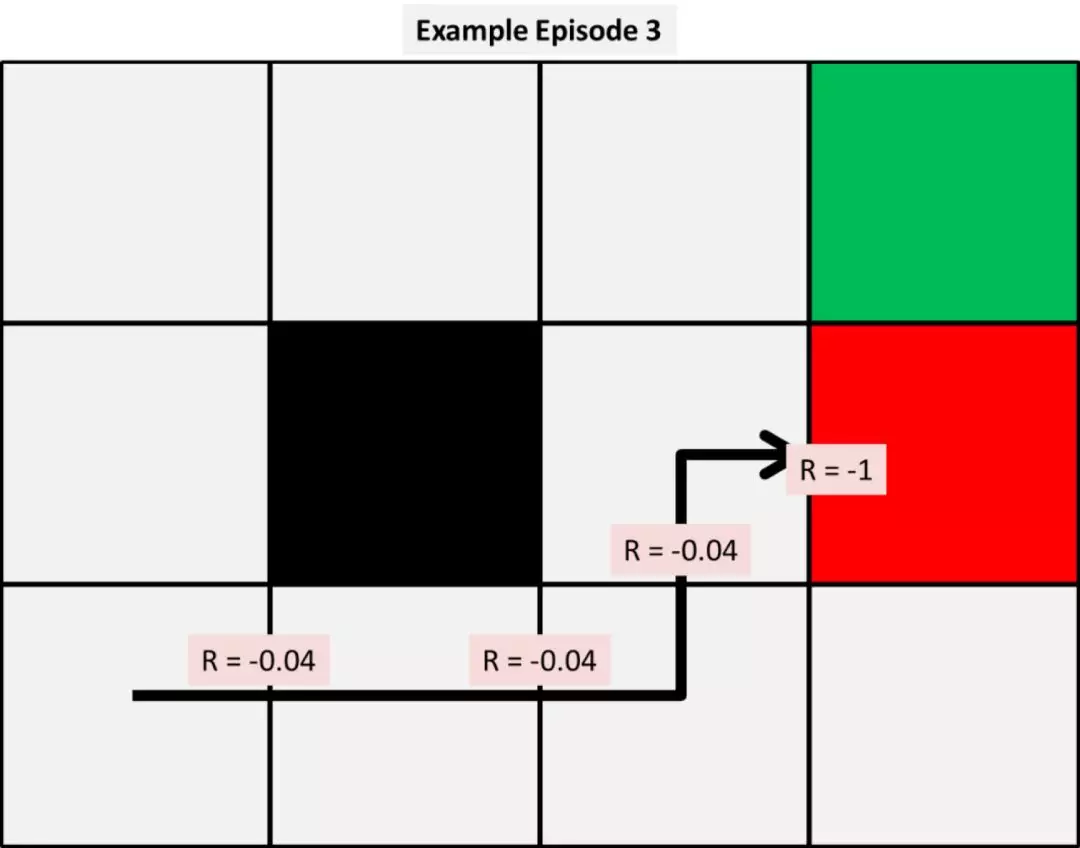
根据这些运行情况,我们可以使用给定的三个模型分别计算状态值函数的前几次变化。为了简化计算,我们把 α(alpha) 和 γ(gamma) 两个参数都设定为 0.5。我们将在之后研究这些参数的不同取值会对结果造成什么影响。
*译注:作者在这里应该采用的是 TD 预测法(TD Prediction),其中最简单的TD方法为 TD(0),它的更新公式为:
V(St) ⇐ V(St)+α[Rt+1+γV(St+1)−V(St)]
其中 V(St) 为当前状态的值,V(St+1) 是记忆里的下一个状态的预测值。α 是学习速率,γ 是折扣因子,Rt+1 为预计动作的即时奖励。
首先,我们按照前面三个回合的结果,用 TD(0) 方法计算出动作价值表:
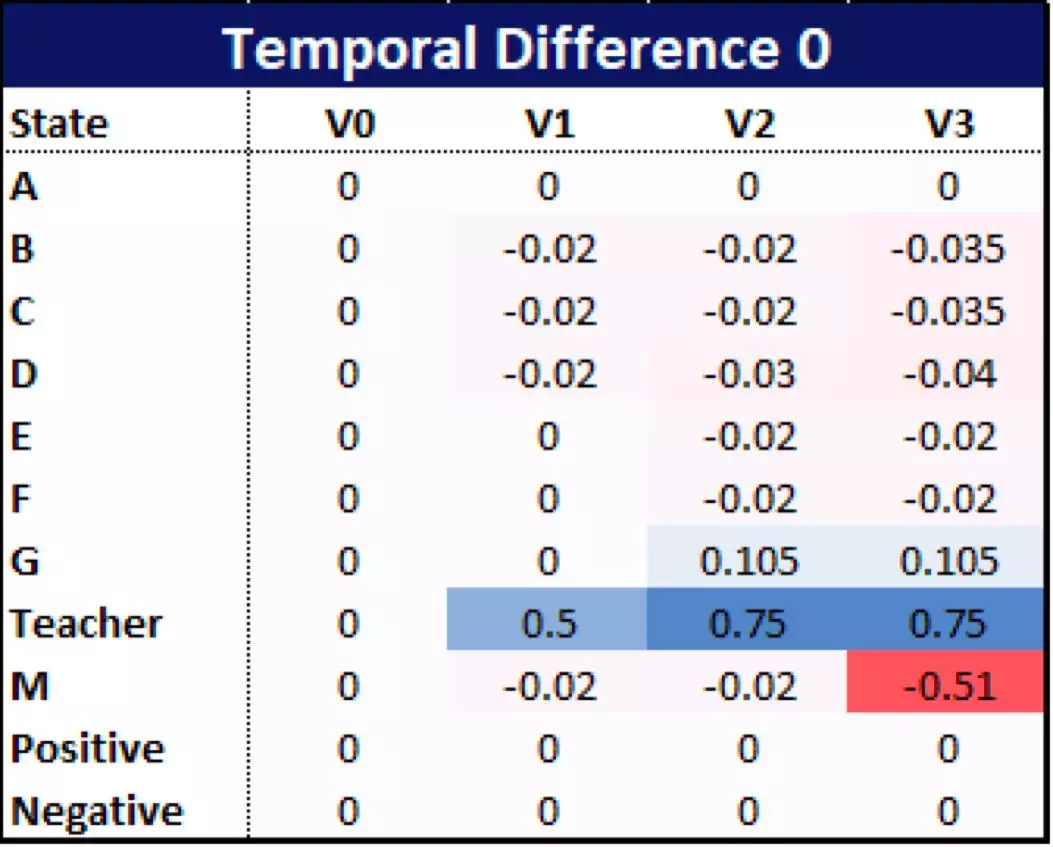
这些数据是怎么来的呢?由于例子中的数据量很小,这里可以手算给大家看:



*译注:请参考前面的 TD(0) 更新公式。
那么,我们从这头几次的运行结果中能看出什么来呢?首先,使用 TD(0) 方法对有一些状态(比如本例中的 D)是不太公平的。
在目前状态下,虽然纸张在 3 次中有两次成功传递到了老师手上,但 D 并没有获得任何奖励。他的价值数字只受下一步的人影响。不过这也显示出正向或负向的终止奖励所产生的影响,是如何从一个角落向所有状态传播的。大致如下图所示:
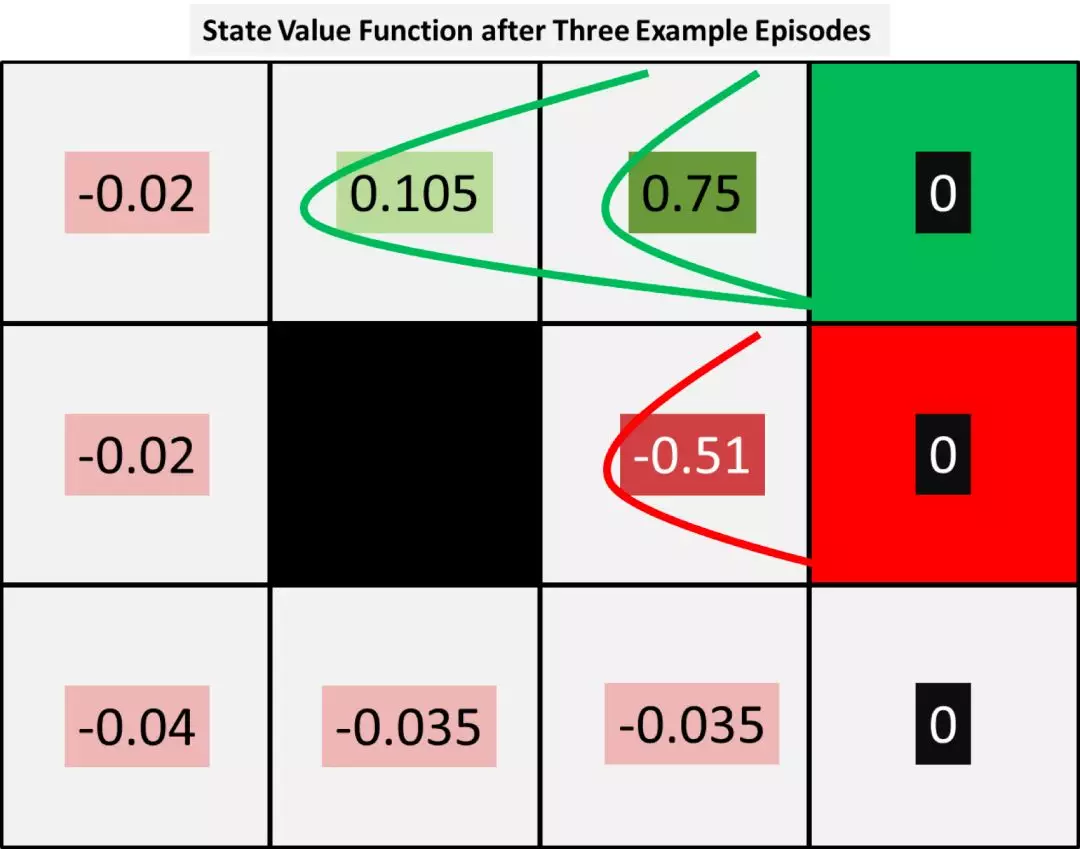
如图所示,两次正向终止奖励所带来的积极影响已经扩散到老师和 G 身上,而M也因为一次负向奖励而受到了惩罚。
随着运行的回合越来越多,这些正向和负向的效应将在所有状态之间扩散。
为了显示出扩散效应,我们可以运行更多回合。我们把开头的三个回合重复运行 9 次,就得到了下面这张表:
(请注意:我们为了简化计算,只是单纯重复了开头的 3 个回合。而在实际项目中,回合运行应该根据观测得到的转移概率函数随机产生。)
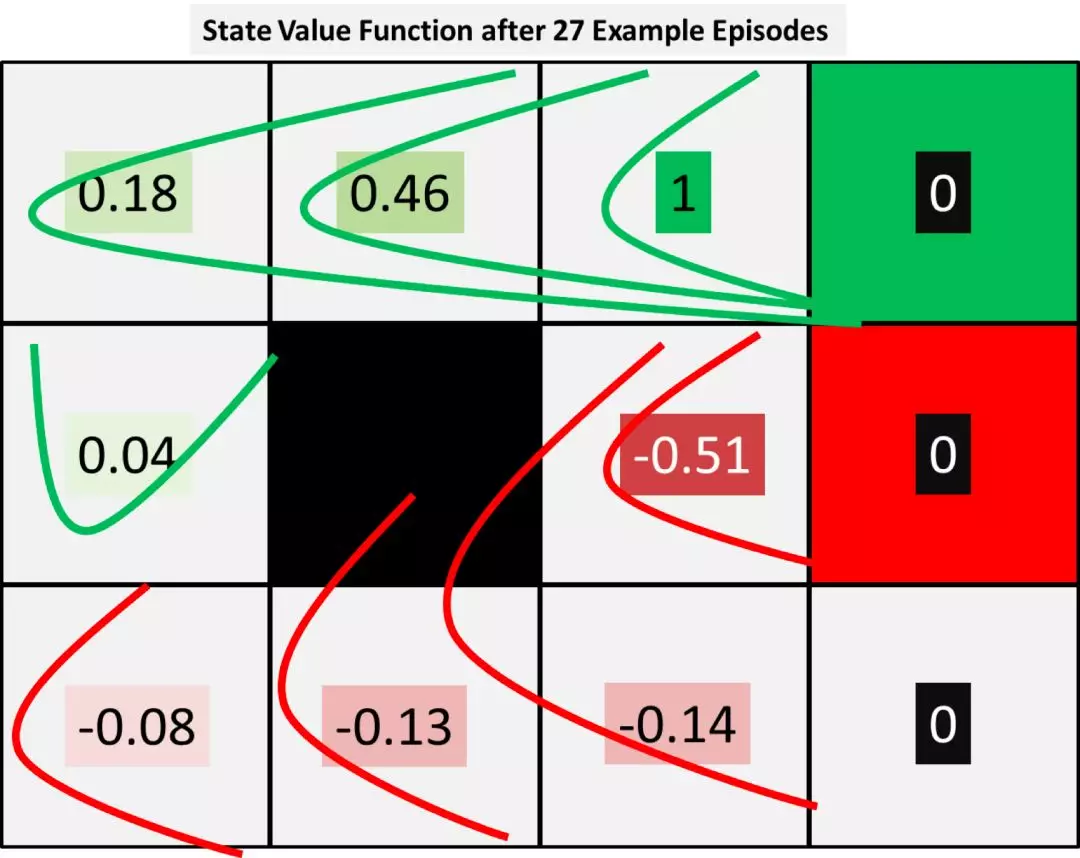
上图显示出,在 27 个示例回合后,终止奖励从右上角传播到了所有状态身上。为此,我们可能需要对策略进行修改,因为很明显从M身上传出的负向奖励已经扩散到 B 和 C 身上了。
于是,基于 V27 的结果,我们对策略表进行如下修改,让行动方向指向临近格中数值最高的方向:
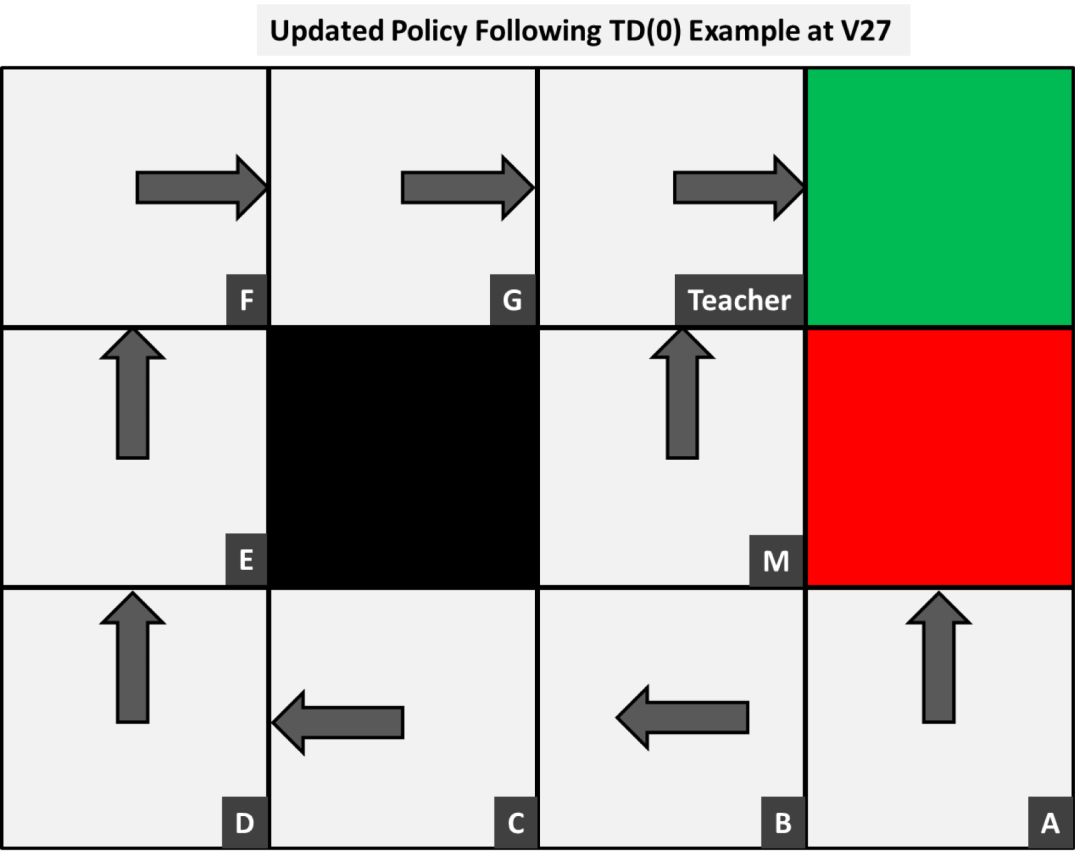
现在我们的模型还有两个问题。
一是 A 的最佳策略还是直接将纸往纸篓方向投。
这主要是因为之前的回合一直没有探索到 A,开启这个“多臂老虎机”问题。在我们的例子中,因为总的状态数并不多,我们可以使用许多回合来确保A被探索到。
至于为什么选择投向废纸篓,这是因为红色和绿色的终止节点本身并没有任何值(它们会导致正向或负向的终止奖励,但它本身的值为0),这导致 B 的值 -0.14 小于 0,于是策略就将动作指向了废纸篓。
对此,如果情况允许的话,我们可以根据最后的结果,用终止奖励的值来初始化 V0 中的这两个终止状态。
二是 M 状态的值随着回合的增加,一直在(大约)-0.03 和 -0.51 之间跳跃,我们需要找到具体原因。
这主要是学习速率 α 变量导致的。目前,我们只是简单地使用了这些参数(α 是学习速率,γ 是折扣因子),还未详细解释它们对结果会产生怎样的影响。
较高的学习速率可能会导致结果不断震荡,反之,太小的学习速率会使结果永远无法收敛。从下图中可以看出,每个回合的总价值V(s) 随着回合的增加,总体上呈上升趋势,但在不同的回合之间还是会不断震荡。
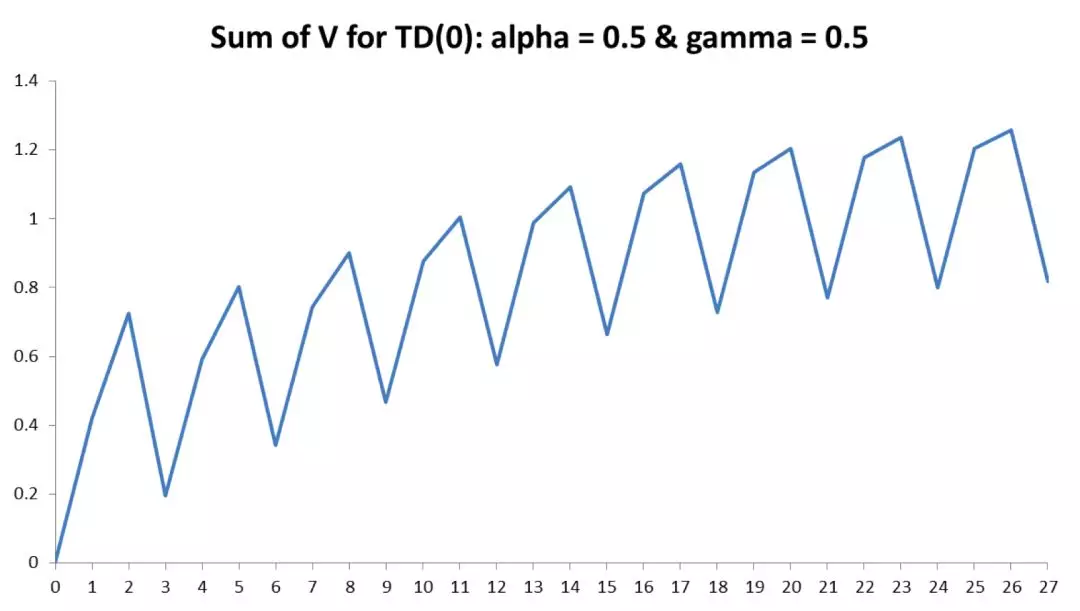
对于学习速率,另外一个很好的解释是这样:
“在高尔夫比赛中,当球离球洞还很远的时候,选手会非常用力挥杆击球,让球尽量飞近球洞;当球打进旗子附近的果岭区域时,选手会换一根不同的球杆,以便打出准确的短球。 因此,这并不是说他不选择对应的球杆就不能把球打进洞里——他可能需要试上两三次才能把球送进目标。但如果他选择最优的状态,使用适当的力道将球打入洞中,那就最好不过了。”
要想确定某个特定问题的最佳学习速率,你可以用一些复杂的方法来计算;但就像任何机器学习算法一样,如果环境足够简单,你可以遍历各种不同的值,直到结果收敛为止。这被称为随机梯度下降法(stochastic gradient descent,SGD)。
我曾经在最近的一个机器学习项目中用动画演示过减少学习速率 α(Alpha)时的影响,如下图所示,当 α 较大时,图形振荡幅度较大,随着 α 的减小,图形变得更加平滑。
同样地,我们也需要指定一个在0到1之间的折扣因子 γ(gamma),常用值一般接近0.9。折扣因子将会告诉模型未来的奖励有多重要:较大的数字表明,模型将会更加重视未来的回报,而将这个数字向零靠拢,则意味着模型将更少考虑未来的步骤。
在理解了这两个参数之后,我们将学习速率 α 从 0.5 降到 0.2,同时将折扣因子 γ 从 0.5 上调到 0.9,则运行得到下面这样的结果:
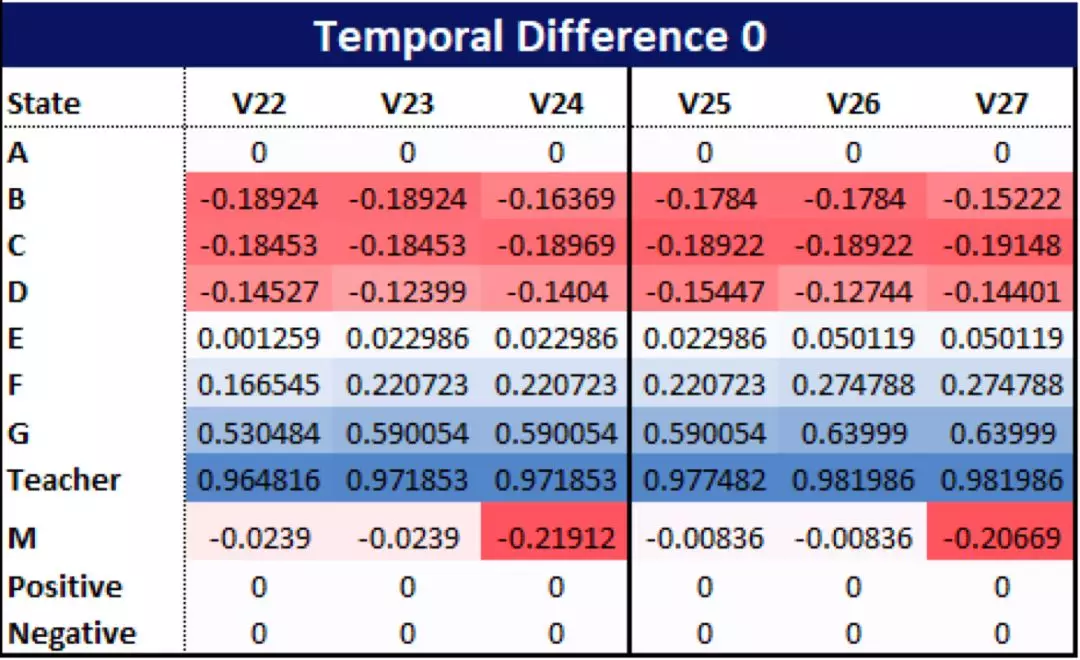
由于新的学习速率更小,模型需要花上更多的回合来学习,生成的值一般也相对较低。
最明显的是,老师肯定还是价值最高的状态,而在消耗更多计算时间作为代价之后,M 的值也不再像以前那么大幅度波动了。
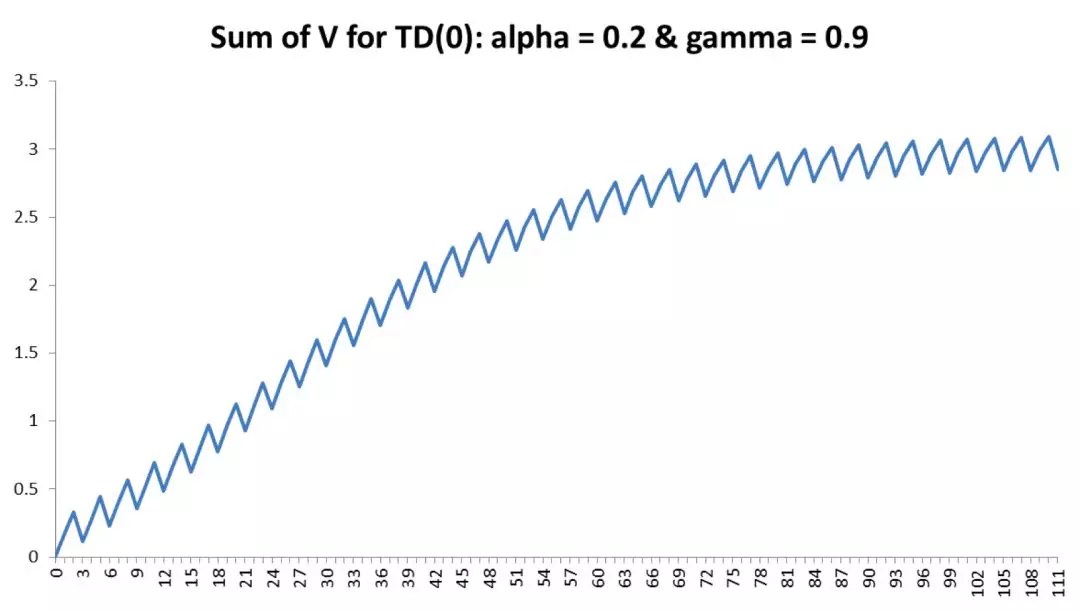
在下图中,我们可以看到,更新参数之后 V(s) 的和随着回合增加的变化情况。虽然还不算非常平滑,但 V(s) 的总和以一种比之前更平缓的速度缓慢增长,并似乎在大约 75 个回合的时候达到了收敛,就像我们期望的那样。
05. 变化的目标结果
强化学习的另外一个关键优势在于,我们可以部分地控制环境。
目前,奖励是基于我们认为模型要如何以尽量少的步骤达到正向结果而设定的。但当环境变化时,比如说老师换了,新来的老师不介意学生把纸张投进废纸篓——只要能进去就行。
于是,我们就要围绕这个新变化修改我们的负面奖励,而最优的策略也会跟着改变。
这在解决业务问题的时候特别有用。比如你正在计划一个策略,并且已经知道有些变化的预期比其他的少,那么你的模型也能将这些纳入考虑,并根据需要进行改变。
最后
现在,我们已经根据观测到的数据,构建了一个简单的强化学习模型。
还有许多需要改进或值得深入讨论的地方,包括使用更复杂的模型等。但对于那些希望尝试并将其应用于解决现实问题的人来说,这已经是一个不错的开始啦。

摄影:Steve Johnson,图片来源:Unsplash
(本文已投稿给「优达学城」。 原作: Sterling Osborne 翻译:欧剃 转载请保留此信息)
编译来源: https://towardsdatascience.com/reinforcement-learning-for-real-life-planning-problems-31314491e5c
标签:Udacity、Translate、Machine-Learning
